Research Objective
The modern landscape of fundamental physics is dominated by quantum theories. Non-relativistic quantum mechanics is used to describe low-energy systems, while quantum field theory is the standard framework for high-energy physics. Quantum theories are so empirically successful that, nowadays, there is a wide consensus about the fact that the fundamental description of the gravitational field must be quantum as well. Given that, according to general relativity, the gravitational field has to be identified with the spacetime structure, this consensus goes as far as accepting that space and time themselves exhibit quantum connotations at the fundamental scale.
However, all quantum theories—whether relativistic or not—have to face a plethora of conceptual problems, irrespective of their predictive success. In particular, there are two questions that the quantum formalism used by physicists is unable to address: First, how can the stable and determinate features of the world, such as macroscopic material structures, be accounted for by a dynamics that just deals with the linear and unitary evolution of the wave function? Second, what is the nature of the wave function itself? Is it a concrete object, like a field, or just a bookkeeping device that accounts for our expectations about measurement outcomes? These issues are rigidly translated to the main quantum gravity programs. For example, how is classical spacetime, with its well-defined geometric structure, supposed to emerge from a superposition of quantum-gravitational states? Or, what does the universal wave function appearing in the Wheeler-DeWitt equation represent? The consequence of these issues is that the picture of the physical world suggested by quantum theories is somewhat obscure, which is a severe drawback if we want to take these theories at face value in a scientific realist spirit.
Usually, this conceptual obscurity is taken to imply the need for an interpretation—which, simply speaking, means supplying the quantum formalism with a clear metaphysics. This line of reasoning, however, leads to an inflation of radically different yet mostly empirically equivalent fundamental ontologies for the quantum world. This abundance of choices, in the end, exacerbates the problem because it adds a further layer of discord to the debate, which cannot be adjudicated by using empirical evidence. This many-faceted controversy is not just philosophical but is also reflected in the way research programs in physics are conducted. In this respect, the most remarkable example is the ongoing branching of the field of quantum gravity into different directions, with no convergence toward a unified approach in sight.
The present project aims to overcome this impasse by elaborating a novel framework for fundamental physics that explains the nature and origin of the “quantumness” of the world instead of just assuming it ab initio. This goal will be achieved through a bottom-up strategy, which can be summarized in three simple steps: 1. Start with well-known classical models, individuate the features X that are strictly necessary to make physical sense of them, and discard all the rest. 2. Repeat the same procedure with quantum models, adding the constraint that they should recover X in the appropriate limit, thus getting a minimal set of quantum properties Y. 3. Construct a quantum gravity model, which possesses the minimal amount of structure required to get X and Y in the appropriate limits.
Significance of the Project
The project introduces a novel research perspective in that it assumes that the objective of elaborating a new framework for fundamental physics cannot be straightforwardly decomposed into a technical and a philosophical component. Establishing the formal setting needs some initial input from metaphysical theorizing, and, at the same time, the choice of ontic commitments compatible with the fundamental aspects of the physical world has to be underpinned by the mathematical structure of the model(s) supposed to represent this world. As such, the project represents an unconventional endeavor for both the theoretical physics and the philosophy of physics communities—where the former privileges a “shut up and calculate” approach to fundamental physics, and the latter usually elaborates on already existing physical approaches. Therefore, if successful, the project would establish a new paradigm in approaching fundamental physics, according to which physics and metaphysics should be treated as a seamless whole. In order to attain this new research perspective, two shifts in paradigm are required.
The first shift involves physical theorizing and consists of adopting a novel framework for mechanics called Pure Shape Dynamics (PSD). This framework is philosophically informed by a peculiar form of relationalism, according to which space comes from a relational ordering of the basic elements of the ontology (spatial relationalism), and time is an abstraction from the ordering of kinematic configurations (temporal relationalism). Hence, PSD represents a natural evolution of the Leibnizian and Machian ideas originally put forward Julian Barbour and Bruno Bertotti, which eventually led to the framework of Shape Dynamics (SD).
PSD implements a two-step procedure for constructing a physical model. First, the configuration space of the physical system under consideration is stripped of all redundant or unobservable degrees of freedom via a “quotienting out” operation. This operation translates the original configuration space onto a purely relational one, called shape space. Such a designation points to the fact that, for any initial non-relational configuration considered, the quotienting out operation removes all redundant spatial degrees of freedom and leaves just a conformal structure, which means that only the shape of the original configuration carries physically meaningful information. The second step consists of implementing the dynamics of the system. This is done by encoding the system’s physically meaningful degrees of freedom in the geometric degrees of freedom of an unparametrized curve in shape space. This latter feature marks the essential difference between PSD and standard SD: Whereas SD involves a notion of parametrized curve, which translates into an extra degree of freedom that is external to the system, PSD dispenses with the need for a parametrization altogether. The choice of PSD in the context of the project is motivated by the following two facts. First, this framework, albeit in its infancy, is fairly well-developed both technically and conceptually. Second, the two-step model construction procedure that characterizes the framework can be applied to any physical system: As long as a system has an associated symmetry group accounting for its redundant/unobservable degrees of freedom, the quotienting out operation can be consistently applied to it. This feature of PSD makes it possible to frame the project as a conceptually unified progressive development of physical models, starting from classical gravitational systems, continuing with quantum fields, and ending up with the quantum gravity model. However, without input from metaphysics, such a model construction strategy would be just an abstract exercise in mathematical physics. In other words, each model should be developed in parallel with an appropriate ontology representing what that model is about (“in parallel” meaning that both the technical and the metaphysical constructions should be refined and updated in concordance as the model-building procedure progresses). This complementarity of physics and philosophy in the context of the project justifies the second change in paradigm, which concerns metaphysical theorizing.
This new perspective comes from the realization that PSD models have very weak spatial and temporal connotations already at the classical level: Relational configurations are individuated and characterized in purely intrinsic terms without any need to embed them in an external spacetime. Plausibly, even thinner spatiotemporal notions will be available for quantum models, with spacetime eventually disappearing in the quantum gravity model. It is then evident that applying the conceptual tools of standard analytical metaphysics, which rely on spatiotemporal intuitions, would cut no ice in this context. For example, concrete objects are usually characterized as being located \emph{somewhere at a certain time}; otherwise, it would be impossible to distinguish them from, e.g., abstract objects. This motivates the enterprise of developing a new type of metaphysical theorizing that relies much less—if at all—on inherently spatiotemporal notions. The need for such an enterprise has been recently recognized by philosophers of physics, and hence, it is a timely endeavor to be undertaken. The project will contribute to this new line of research by developing a non-standard account of relational configurations that merges monism and ontic structural realism. This account rests on a novel understanding of dependence relations in fundamental physics, which goes beyond the usual analyses of determination given in terms of causation, grounding, or composition.
Work Plan
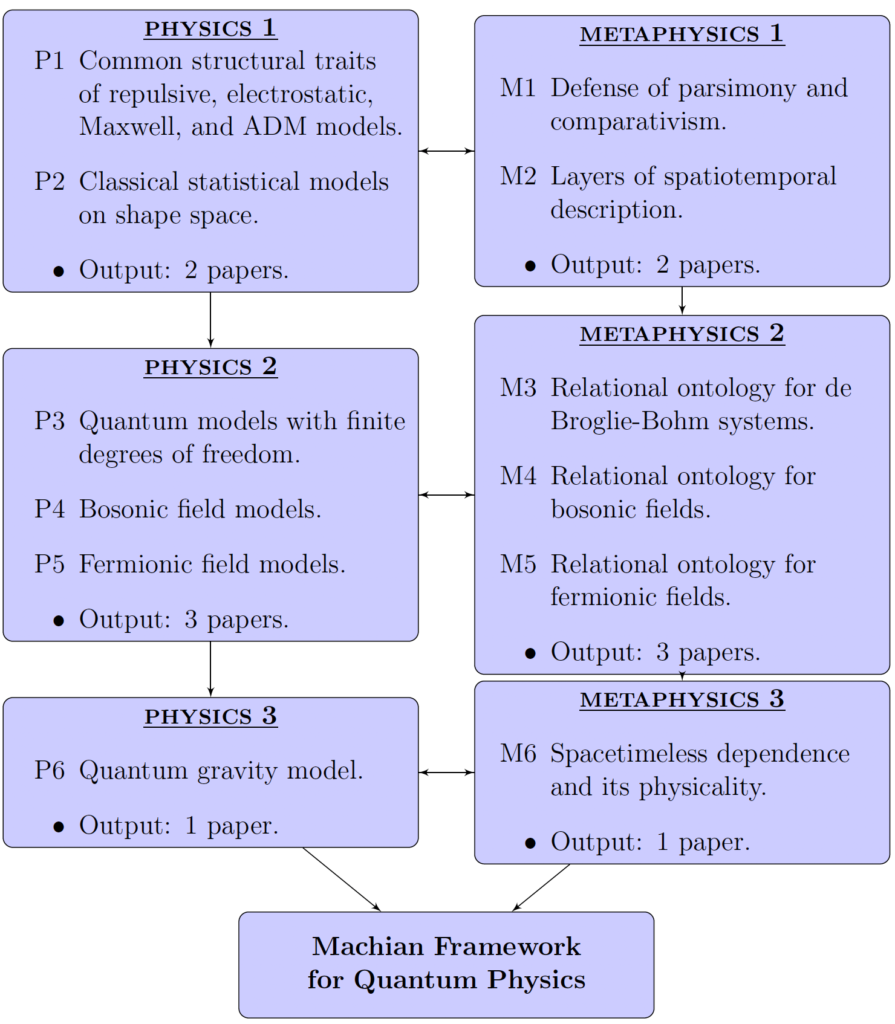
The project’s research plan consists of implementing these changes in paradigm in two deeply interconnected sub-projects named *Physics* and *Metaphysics* to be carried out in 36 months. Each sub-project consists of three work packages involving a total of six tasks. Each completed task will be summarized in a paper to be submitted to a top-level journal and presented to the scientific community at international events.
The work package *Physics 1* will start with constructing the PSD description of a set of classical models and analyzing their common traits in order to highlight the structural origin of their phenomenology (task P1). The research will focus on three classes of models, namely, (i) some extensions of the Newtonian N-body problem that include short-range attractive/repulsive forces, (ii) the classical Maxwell field, and (iii) ADM gravity. All these systems have well-defined and well-known symmetry properties, and hence, they are amenable to the two-step procedure described above. Particular attention will be paid to some remarkable physical features exhibited by this PSD description, the most important of these being the existence of a measure—dubbed complexity functional—for the ability of the system to store information in local subsystems through structure formation. This functional permits to order the different stages of the system’s dynamical evolution in terms of its increasing complexity without invoking an external temporal labeling. The complexity functional plays an essential role in recovering more structured spatial and temporal notions, such as scale and duration, from the underlying relational dynamics through mathematical constructions called ephemeris equations. These equations represent the link between the fundamental relational dynamics and the usual physical description of a system in fully spatial and temporal terms. Moreover, to set the stage for the quantum extension of the framework, some classical statistical models on shape space will be investigated (task P2). The purpose of these models is to identify two ways to express a measure of incongruence among shapes, one based on trajectories and the other based on ensembles. The goal of this task is to pinpoint the structural differences between these two formulations at the classical level, which will later be exploited when constructing the quantum models, including quantum gravity.
The work package *Metaphysics 1* will provide a sharp metaphysical analysis of the classical models developed in *Physics 1*. First, the quotienting out procedure used to reach a fully relational configuration will be interpreted as a “parsimonization” of the ontology of the system, whereby all ontic commitments to redundant and unobservable features are removed. It will be argued that such a removal is best conceived of as an ontological reduction of spatiotemporal facts to facts about shapes. Consequently, new arguments will be elaborated in defense of ontological parsimony and comparativism about physical magnitudes (task M1). Secondly, a thorough discussion will be provided of the mechanism through which everyday notions of space and time are recovered from the ephemeris constructions (task M2). Under the light of this reductionist side of the PSD framework, it will be argued that elaborated spatiotemporal notions, such as scale and duration, are just vocabulary shortcuts to refer to fundamental relational facts regarding shapes—in particular, facts about shape complexity and its variation throughout a dynamical curve. Collectively, the first stage of the project will be carried out in 9 months.
Once a good understanding of the classical models’ features of PSD is acquired, the project will move forward by inquiring how these notions have to be revised when constructing quantum models. This part of the project marks the entrance to a totally uncharted territory since very little is known at the moment about possible quantum versions of relational theories à la Barbour-Bertotti. The work package *Physics 2* is concerned with the technical implementation of these quantum models. Given the novel and challenging nature of the task, the implementation strategy will involve three approaches to be pursued in parallel to maximize the chances of success. The first—and safest—approach will be based on de Broglie-Bohm trajectories in shape space since these are conceptually similar to classical curves in shape space. This will guarantee that the two-step construction procedure can be carried over to the quantum context. The second approach is slightly riskier and will be based on a polar decomposition of the wave function in shape space, so as to obtain a classical probability distribution evolving under the influence of a phase functional on shape space. Investigating this construction is interesting in that it is analogous to the construction of classical probability theory on shape space. The third approach is concerned with a Schrödinger-type wave equation that evolves from lower-complexity surfaces in shape space to higher-complexity ones. This approach is the most relational among the three in that it implements the idea that temporal development is abstracted from the instantaneous amount of information about the past carried by the shape of the universe. These three approaches will be applied to constructing increasingly refined quantum models, starting from quantum mechanics with finite degrees of freedom (task P3), continuing with quantum field theories of bosonic fields (task P4), and finally including fermionic fields (task P5).
The work package *Metaphysics 2* will be developed in parallel with *Physics 2* and will start with a reflection on the notion of local beables—an expression that refers to material entities located in space and time. Since all empirical evidence is ultimately couched in terms of local beables (e.g., readings on a display), any empirically adequate—and ontologically clear—physical theory has to provide a coherent story about how a description of the world in terms of local beables is arrived at. Consequently, the main aim of *Metaphysics 2* will be to characterize quantum shapes and link them to the appearance of local beables without presupposing spatiotemporal notions, in light of the model construction carried out in *Physics 2*.
The first step will be to recognize that, in the classical case, a shape can be described as a “web” of weak spatial relations among some appropriate relata. Two stances compatible with this fact will be considered: Priority monism, according to which a shape as a whole is more fundamental than its constituents, and moderate ontic structural realism, which maintains that a shape is made up of a set of relations and relata that must be considered on par from an ontological viewpoint. The analysis will focus on the role that a spatiotemporally grounded mereological structure plays in establishing a directed relation of dependence between the shape as a whole and its constituents. It will be argued that the less spatiotemporal notions are involved, the weaker the mereological structure becomes, thus making the part/whole dependence direction ever less well-defined as space and time fade from the picture.
It will then be noted how the quantum version of the quotienting out procedure translates to a radical parsimonization of the ontology, whereby shapes become structures held together by entanglement relations: This is how the non-locality of quantum physics is rendered in this context. The picture of shapes as entanglement structures washes away any remnant of spatial connotation from the ontology, thus making monism and structuralism collapse into a single stance when quantum shapes are considered. Then, the process of formation of beable-like subsystems from whole shapes will be explained in purely functionalist terms by claiming that subsystems are not genuine entities but partial descriptions of how a shape dynamically evolves. The project will argue that the proposed metaphysics essentially differs from a primitive ontology approach because it does not need to take any sort of beable as fundamental. This thorough metaphysical investigation will be carried out for each of the models developed in *Physics 2*, thus coming up with a three-step characterization of the ontology of quantum relational systems (tasks M3, M4, and M5). This second stage of the project will be completed in 18 months.
Finally, *Physics 3* will attempt to construct a PSD model of quantum gravity (task P6). The natural strategy is to take the conformal metric—the major ingredient of the PSD description of classical dynamical geometry—and work out the corresponding quantum field theory along the general principles set out in *Physics 2*. The notion of structure formation underlying the complexity functional will be studied in this context, pointing out how it eases the physical interpretation of the dynamics. Particular attention will be paid to the degrees of freedom pertaining to quantum models that can be further quotiented out in this context as irrelevant, thus constituting the quantum features that appear as a phenomenological result of the quantum gravitational dynamics. This is where a better understanding of the origin of the “quantumness” of the physical world is expected to be achieved.
Given that the quantum gravity model will likely dissolve the classical conformal structure into a network of entanglement relations, *Metaphysics 3* will elaborate an account of the non-spatiotemporal determination relation linking the quantum-gravitational degrees of freedom to the “emergent” phenomenological ones (task M6). The proposed account will exploit a variant of the structural equation modeling framework, which has recently been applied to the analysis of spacetime/matter dependence in general relativity. The goal of the task is to characterize the novel type of determination involved and explain why it qualifies as physical as opposed to a mathematical construction. This third stage of the project will be completed in 9 months.
The project’s outline, including task dependencies, is given below:
Research Methodology
The research methodology will involve a conceptual investigation firmly rooted in the scientific method and the analytic philosophy tradition. Given that the primary research questions tackled come from the framework of modern physics, the type of philosophical inquiry conducted will reflect a naturalized attitude towards metaphysics, that is, the conviction that fruitful metaphysical research must be motivated and informed by science.

